Constante de los gases ideales

La constante universal de los gases ideales, constante de los gases o constante molar de los gases^[1]​^[2]​^[3]​ es una constante física, más concretamente termodinámica, que establecida inicialmente en relación con variables del estado gaseoso: volumen, presión, temperatura y cantidad de sustancia, ha devenido en una constante de gran importancia en campos más amplios.

Introducción

En su forma más particular la constante se emplea en la relación de la cantidad de materia en un gas ideal, medida en cantidad de sustancia (n), con la presión (P), el volumen (V) y la temperatura (T), a través de la ecuación de estado de los gases ideales:^[4]​^[5]​^[6]​^[7]​^[8]​

${\displaystyle PV=nRT}$

El modelo del gas ideal asume que el volumen de la molécula es cero y las partículas no interactúan entre sí. La mayor parte de los gases reales se acercan a esta constante dentro de dos cifras significativas, en condiciones de presión y temperatura suficientemente alejadas del punto de licuefacción o sublimación. Las ecuaciones de estado de gases reales son, en muchos casos, correcciones de la anterior.

Valor de R

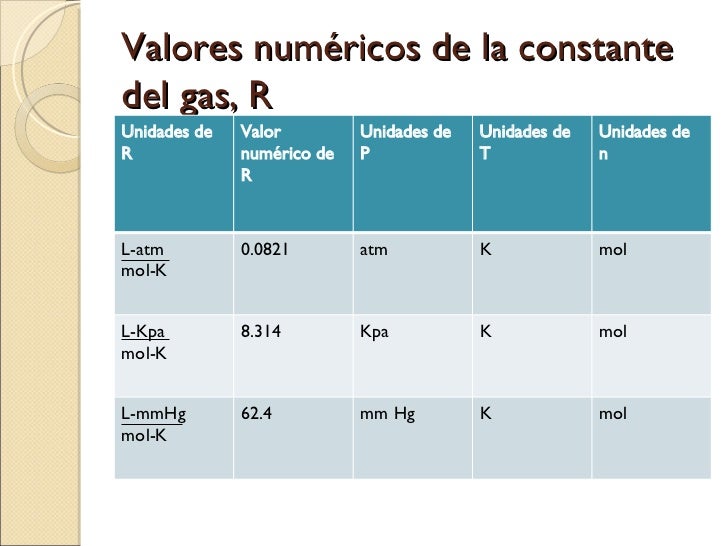
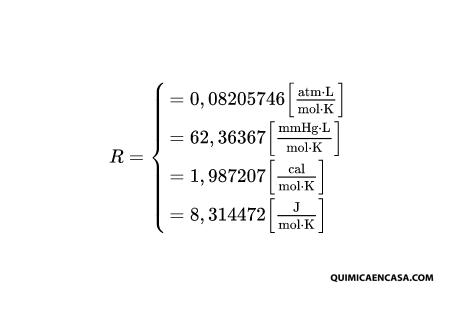
El valor de R en distintas unidades es:

${\displaystyle R={\begin{cases}=0,08205746\mathrm {\left[{\frac {atm\cdot L}{mol\cdot K}}\right]} \\=62,36367\mathrm {\left[{\frac {mmHg\cdot L}{mol\cdot K}}\right]} \\=1,987207\mathrm {\left[{\frac {cal}{mol\cdot K}}\right]} \\=8,31446261815324\mathrm {\left[{\frac {J}{mol\cdot K}}\right]} \\\end{cases}}}$

Relevancia

Si bien la constante se introdujo originalmente en el contexto de los gases, y de ahí su nombre, la constante R aparece en muchos otros contextos que no tienen relación con los gases. Esto se debe a que, la constante R está relacionada con la constante de Boltzmann, que es un factor que relaciona en muchos sistemas unidades de energía con unidades de temperatura. De esta manera, cuando la relación se establece con la cantidad de materia entendida como número de partículas, se transforma la constante R en la constante de Boltzmann, que es igual al cociente entre R y la constante de Avogadro:

${\displaystyle k_{B}={\frac {R}{N_{A}}}}$

Como desde 2019 las constantes de Boltzmann y de Avogadro fueron definidas con valor exacto, ello hace que R también tenga un valor exacto. Además de en la ecuación de estado de los gases ideales, la constante universal R (o en forma de constante de Boltzmann) aparece en muchas expresiones físico-químicas importantes, como la ecuación de Nernst, la de Clausius-Mossotti (conocida también como de Lorentz-Lorentz), la de Arrhenius, la de Van't Hoff, la ley de Dulong-Petit, así como en termodinámica estadística.

Véase también

• Ley de los gases ideales
• Ecuación de Van der Waals
• Ley general de los gases
• Constante de Avogadro
• Teoría cinética

Referencias

Bibliografía

• Peter J. Mohr, and Barry N. Taylor, "CODATA recommended values of the fundamental physical constants: 1998", Rev. Mod. Phys., Vol 72, No. 2, April 2000
• Levine, I.N. “Physical Chemistry ” (4ª ed.), McGraw-Hill, New York, 1996. “Fisicoquímica” (trad. A. González Ureña, versión de la 4ª ed.), McGraw-Hill/Interamericana, Madrid, 1999.
• “Introducción a la Termodinámica en Ingeniería Química”. J.M. Smith J.M. y H.C. Van Ness. 7a Ed. Mc Graw-Hill

Enlaces externos

• Gas Constant CODATA Value at NIST
• Boltzmann Constant CODATA Value at NIST